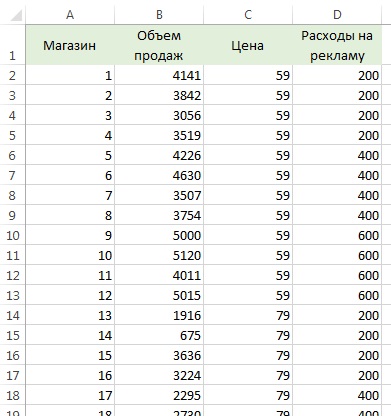
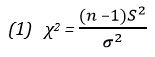Принятие решений
Ранее мы изучили различные правила вычисления вероятностей, а также применили теорему Байеса для уточнения вероятностей с учетом новой информации. Кроме того, было введено понятие дискретного распределения. Теперь мы используем эти правила и теоремы для выбора конкретного плана действий. Процесс принятия решений характеризуется четырьмя основными свойствами. [1]
- Альтернативные планы действий. Прежде чем сделать окончательный выбор, лицо, принимающее решение, должно оценить несколько вариантов. Например, менеджер взаимного фонда в описанном ниже сценарии должен решить, покупать акцию А или Б.
- События или экономическое положение. Лицо, принимающее решение, должно перечислить возможные события и вычислить их вероятность. Например, для того, чтобы правильно выбрать компанию при покупке акций, экономист взаимного фонда перечислил четыре возможных сценария развития экономики в течение следующего года и указал их вероятность.
- Таблица выигрышей. Для того чтобы оценить план действий, лицо, принимающее решение, должно сопоставить каждому событию возможный выигрыш или проигрыш. В деловых приложениях выигрыш и проигрыш обычно выражаются в терминах прибыли или убытка, хотя существуют и другие формы, например, моральное удовлетворение или польза. При покупке акций выигрыш выражается в виде доходности инвестиций.
- Критерий принятия решения. Лицо, принимающее решение, должно установить критерий выбора наилучшего плана действий. В заметке рассмотрено несколько таких критериев.