8. Статистика

Квартиль — одна из статистик, используемая при описании выборок (подробнее о различных статистиках см. Определение среднего значения, вариации и формы распределения. Описательные статистики). В то время как медиана разделяет упорядоченный массив пополам, квартили разбивают набор данных на четыре части. Первый квартиль – это число, разделяющее выборку на две части: 25% элементов меньше, а 75% — больше значения первого квартиля. Третий квартиль — это число, разделяющее выборку также на две части: 75% элементов меньше, а 25% — больше третьего квартиля.

Рис. 1. 5-числовые сводки: М – медиана, Н1 и Н2 – сгибы (они же квартили)

Подробнее »КВАРТИЛЬ: какие формулы расчета использует Excel

Начну с того, что мне очень интересен байесовский подход. Много читал, чтобы осмыслить его (см. литературу в конце заметки), и могу засвидетельствовать, что постигнуть его непросто… А недавно, прочитав книгу Герд Гигеренцер. Понимать риски. Как выбирать правильный курс, обнаружил, что байесовский подход можно дополнить более интуитивным (хотя и менее строгим) методом, который автор назвал естественной частотой.

Рис. 1. Иллюстрация суждений в стиле естественной частоты

Подробнее »Естественная частота против байесовского подхода

Недавно прочитал замечательную книгу Хитосе Кумэ. Статистические методы повышения качества. Книга в первую очередь адресована практикам, причем не только менеджерам, но и рабочим. В книге раскрыты методы сбора и обработки данных для управления качеством (см. также Семь основных инструментов контроля качества). В книге содержится одна глава, посвященная статистическому выводу. С одной стороны, она несколько выбивается из общей канвы книги, с другой стороны, в ней содержится краткий обзор по теме, причем изложенный весьма доходчиво (более подробно см. Левин. Статистика для менеджеров с использованием Microsoft Excel). Собственно, перед вами эта глава с небольшими сокращениями и моими комментариями.

Рис. 1. Место статистического вывода в наблюдениях и вычислениях

Подробнее »Введение в теорию статистического вывода

Начнем с примера. В урне, стоящей перед вами, с равной вероятностью могут быть (1) два белых шара, (2) один белый и один черный, (3) два черных. Вы тащите шар, и он оказывается белым. Как теперь вы оцените вероятность этих трех вариантов (гипотез)? Очевидно, что вероятность гипотезы (3) с двумя черными шарами = 0. А вот как подсчитать вероятности двух оставшихся гипотез!? Это позволяет сделать формула Байеса, которая в нашем случае имеет вид (номер формулы соответствует номеру проверяемой гипотезы):

Подробнее »Формула Байеса

Я уже несколько раз сталкивался с тем, что существуют две статистики, обе называемые стандартное отклонение, для описания меры рассеивания случайной величины. Недавно это произошло при чтении книги Дональд Уилер, Дэвид Чамберс. Статистическое управление процессами. Чтобы эти статистики различать, в книге они названы по-разному. Корень из среднего квадрата отклонения s_n, определен для ряда, состоящего из n элементов формулой:

Стандартное отклонение рассчитывается по формуле:

Подробнее »СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г: в чем различие?

Выбросы — точки, сильно выбивающиеся из последовательности, не вписывающиеся в модель по какой-либо причине. Люди озаботились выбросами, желая избавиться от них. Выбросы оттягивают на себя средние значения и сдвигают распределение данных. [1] Иногда выбросы – просто ошибка ввода. Поэтому первая причина обращать внимание на выбросы — это обеспечение чистоты анализа данных и моделирования. Но есть и другая – определение выбросов интересно само по себе!

Рис. 1. Вероятность 349-дневной беременности

Подробнее »Определение выбросов

Задачи прогнозирования построены на изменении неких данных во времени (продаж, спроса, поставок, ВВП, выбросов углерода, численности населения…) и проецировании этих изменений на будущее. К сожалению, выявленные на исторических данных, тренды могут нарушаться множеством непредвиденных обстоятельств. Так что данные в будущем могут существенно отличаться от произошедшего в прошлом. [1] В этом и состоит проблема прогнозирования.

Однако, существуют методики (под названием экспоненциальное сглаживание), позволяющие не только попытаться предсказать будущее, но и выразить численно неопределенность всего, что связано с прогнозом. Численное выражение неопределенности с помощью создания интервалов прогнозирования поистине неоценимо, но часто игнорируется в прогностическом мире.

Рис. 1. Временной ряд данных

Подробнее »Прогнозирование на основе экспоненциального сглаживания

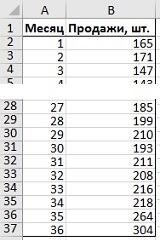
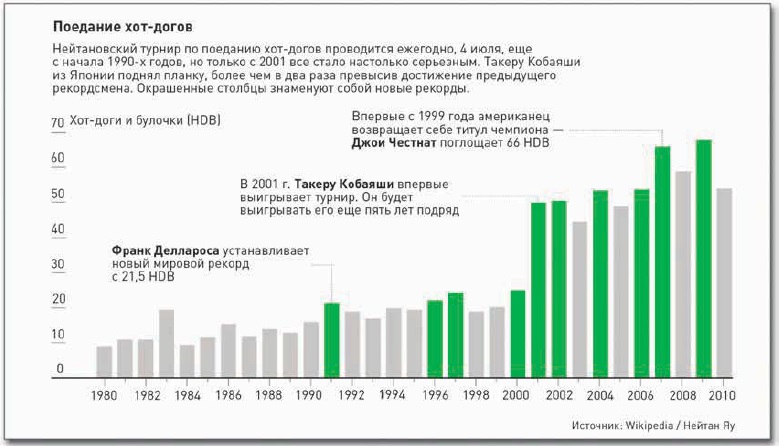
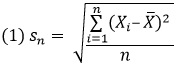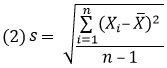Большинство пользователей обратятся к Excel, если нужно построить кольцевую диаграмму. Я тоже в 2012 г. написал на эту тему заметку – Excel. Круговая диаграмма с двумя наборами данных. Однако, около месяца назад я начал читать книгу Нейтана Яу Искусство визуализации в бизнесе. Автор работает в области инфографики, для которой стандартные средства Excel являются недостаточно выразительными. На страницах книги автор знакомит читателей с различными программами, которые расширяют возможности (см., например, Создание столбчатой диаграммы в R).

В настоящей заметке интерактивная кольцевая диаграмма будет построена с помощью программы Protovis. Protovis — бесплатный инструмент для визуализации с открытым исходным кодом. Protovis — это JavaScript-библиотека, позволяющая использовать возможности современных браузеров для работы с масштабируемой векторной графикой. Поскольку графические объекты генерируются динамически, это дает возможность делать их анимированными и интерактивными. А потому Protovis — отличный выбор для создания онлайн-графики. [1]

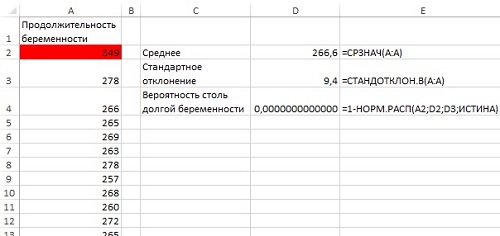
На рис. 1 показано, к чему вы будете стремиться. Когда указатель мыши оказывается поверх того или иного сектора, вы видите, сколько именно человек проголосовало за данную категорию. Интерактив может быть и более продвинутым, но прежде чем давать волю фантазии, необходимо освоить азы.

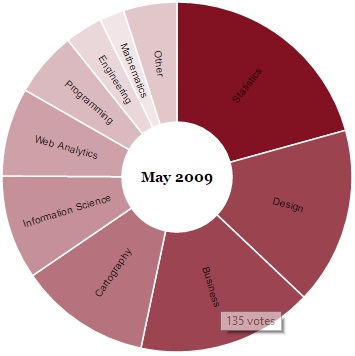
Рис. 1. Интерактивная кольцевая диаграмма, созданная с помощью библиотеки Protovis.js

Подробнее »Интерактивная кольцевая диаграмма, созданная с помощью Protovis

Большинство пользователей (и я в том числе) применяют Excel для построения диаграмм. Однако, возможности Excel относительно ограничены, и в какой-то момент вам вполне вероятно захочется большего. Рассмотрим пример создания столбчатой диаграммы в статистическом пакете R и последующей обработки диаграммы в Adobe Illustrator для придания издательского качества вашей работе. [1] Если вы никогда не сталкивались с R, рекомендую начать с книги Алексея Шипунова Наглядная статистика. Используем R!

В качестве исходных данных возьмем результаты Нейтановского турнира по поеданию хот-догов за последние три десятилетия (рис. 1).

Рис. 1. Окончательный вариант диаграммы, которую вы будете стараться построить; чтобы увеличить картинку, кликните на ней правой кнопкой мыши и выберите опцию Открыть картинку в новой вкладке

Подробнее »Создание столбчатой диаграммы в R

Excel и другие программы, работающие по методу «указал и щелкнул», относительно просты в освоении и покрывают большинство потребностей. Однако, если вы хотите создавать выдающиеся диаграммы и инфографику, вам не обойтись без написания кода для форматирования данных. [1] Посмотрите, как можно легко переключаться с одного формата данных на другой с помощью всего нескольких строчек кода Python.

В качестве исходных данных возьмем файл, полученный путем скрапинга сайта Weather Underground (подробнее см. Извлечение данных с web-страниц с помощью кода на языке Python). Файл wunder-data.txt содержит данные о максимальных ежедневных температурах в Москве за 2015 год (рис. 1).

Рис. 1. Максимальные ежедневные температуры в Москве за 2015 год

Подробнее »Форматирование данных с помощью кода на языке Python