Управление в условиях риска и неопределенности

Нелегкое это дело – предсказывать, особенно будущее…
Йоги Берра

При планировании деятельности возникает неопределенность. А с неопределенностью связан риск. Тем не менее, к риску и неопределенности не следует относиться отрицательно. Это просто оборотная сторона доходности и развития! Как заметил Джин Кэллахан: «Существование деятельности подразумевает неопределенность будущего. В мире, где будущее известно наверняка, деятельность невозможна!»

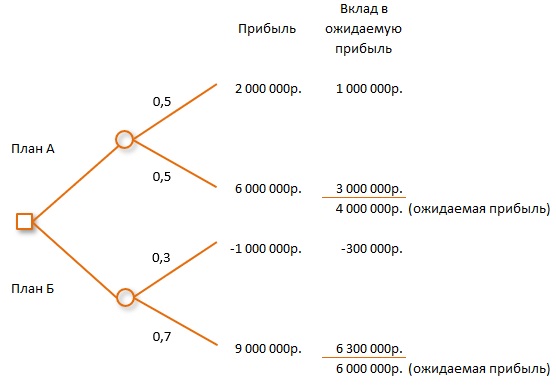
Рис. 1. Пример дерева принятия решений; квадратик – точка принятия решения, кружки – моменты наступления случайных событий

Предыдущая глава Оглавление Следующая глава

Скачать заметку в формате Word или pdf, примеры в формате Excel

Неопределенность – состояние, когда наступление тех или иных событий имеет вероятностную природу. Риск – негативное влияние неопределенности на цели деятельности. Если деятельность осуществляется без постановки целей, то иногда вы не будете знать, реализовался ли риск…

Умение принимать решения в условиях риска и неопределенности – это следующий шаг в развитии управленческих навыков по сравнению с планированием на основе одного (пусть и самого вероятного) сценария. В теории и практике менеджмента используются различные методы принятия решений, учитывающие вероятностную природу будущих событий.

Математическое ожидание

Это самый простой и часто встречающийся способ учета неопределенности. Матожидание рассчитывается путем взвешивания возможных результатов по вероятности их наступления. Например, компания изучает перспективы запуска в производство нового продукта. Решение о запуске будет положительным, если ожидаемый доход превысит 1 млн. руб. Маркетинговые исследования выявили несколько возможных сценариев развития событий (не спрашивайте меня, как маркетологи пришли к таким суждениям :)):

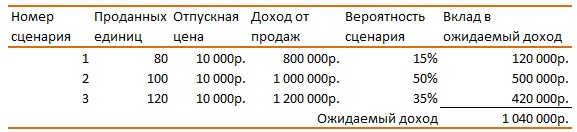
Матожидание дохода = 800 000 * 0,15 + 1 000 000 * 0,5 + 1 200 000 * 0,35 = 1 040 000 руб.

Выделяют три типа отношения к риску:

нейтральные к риску – главное внимание уделяют матожиданию, практически игнорируя возможные отклонения;
склонные к риску – сосредотачиваются на самой благоприятной возможности, меньше внимания уделяя ее вероятности;
не склонные к риску – концентрируются на негативных сценариях, выбирают решения, в которых потери или отклонения от среднего минимальны.

Игра на шансы

Иногда менеджеры ориентируются не на матожидание, а на шансы. Нассим Николас Талеб считает, что такой подход способен порождать Черных лебедей – события малой вероятности, но с катастрофическими последствиями:

Матожидание = 0,999 * 1 – 0,001* 10 000 = -9,001. Но вероятность потери крайне мала. Есть шансы, что мы делали бы деньги, ставя на событие А. Почему люди путают вероятность и матожидание, то есть шансы и вероятность, умноженную на вознаграждение? Главным образом, потому что многие примеры в обучении приходят из симметричного окружения, подобно броску монеты. Природа риска не всегда основана на нормальной кривой. Асимметричные распределения способны скрывать суровую правду жизни.

Дерево решений

Если неопределенности подвержено несколько параметров, вместо матожидания можно построить «дерево решений». Математика метода аналогична, а итоги представляются не в виде таблицы, а графически. Например, могут рассматриваться два альтернативных бизнес-плана:

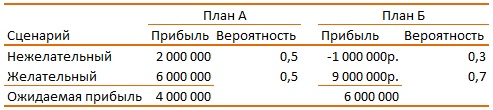
Матожидание плана Б выше. Однако, в нем с вероятностью 30% возможны убытки, в то время как план А всегда генерирует прибыль (см. рис. 1 выше).

Меры разброса

Помимо центральной меры – среднего значения, неопределенность характеризуют и различные меры разброса (или кучности). Стандартное отклонение (оно же среднее квадратичное отклонение):

где i – число элементов в выборке, х_i – значение i-го элемента выборки, х̄ – среднее значение всех элементов выборки, p_i – вероятность i-го события (сумма всех p_i по выборке равна единице).

Для сравнения нескольких выборок используют коэффициент вариации, равный стандартному отклонению, нормированному на среднее значение:

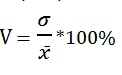
Чем меньше коэффициент вариации, тем более однородной является выборка, тем меньше риски. При анализе финансовых инструментов стандартное отклонение нормированное на период времени выступает там под названием волатильность.

Теория игр

Принятие решения основывается не только на вычислениях. Когда лица, принимающие решения, сталкиваются с выбором между вариантами, они ищут компромисс между риском и доходностью. Поиск такого компромисса затрагивает вопросы поведенческого характера, и основаны на предпочтениях. Например, розничный торговец, обладая ограниченной суммой, может купить у оптовика только один вид фруктов. Торговля с равной вероятностью может пойти по одному из сценариев. Как отношение торговца к риску повлияет на выбор им фруктов?

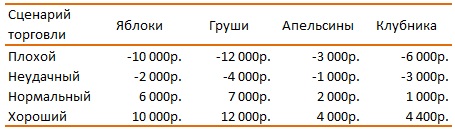
Метод «максимин». Рассматриваются только наихудшие исходы в каждом сценарии. Если наш торговец не склонен к риску, он предпочтет апельсины – МАКСИмальный результат при МИНимальном (наихудшем) сценарии.

Метод «максимакс». А в этом случае упор делается на МАКСИмальный результат при МАКсимальном (наилучшем) сценарии. Если наш торговец склонен к риску, он будет надеяться на хороший сценарий, и выберет груши.

Метод Монте-Карло

Метод развивает подходы, оценивающие вероятность исходов. На первом этапе строят модель, в которой зависимая переменная связана с влияющими переменными. Годовая экономия (зависимая переменная) есть функция трех видов экономии и объема производства (всего четырех влияющих переменных):

На втором этапе задаются правила изменения влияющих переменных. Например, экономия на трудозатратах подчиняется нормальному распределению со средним $3 на изделие, и стандартным отклонением $3,5. Результат моделирования – распределение вероятности годовой экономии:

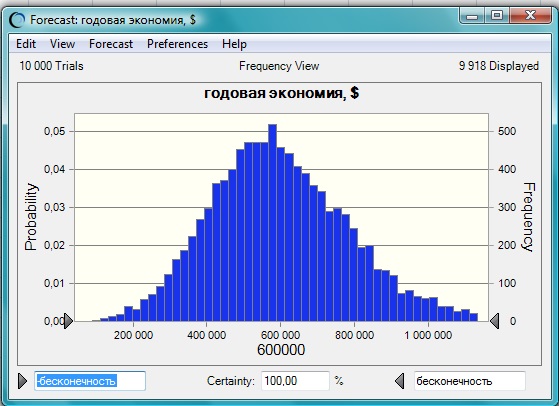
Анализ чувствительности

Оценивает неопределенность, изучая, как влияет изменение ключевых переменных на ожидаемый результат. Анализ затраты–объем–прибыль и анализ безубыточности являются разновидностями анализа чувствительности, поскольку показывают, как меняется прибыль при изменении уровня продаж.

Измерения для уменьшения неопределенности

Почти всегда можно провести измерения, позволяющие сократить первоначальную неопределенность в точке принятия решения. Что и как измерять, а также оправданы ли расходы на проведение измерений изучает Прикладная информационная экономика.

Измерение – один из основных инстинктов человека, однако этот инстинкт подавляется в условиях, когда люди предпочитают создавать комитеты и добиваться консенсуса вместо того, чтобы делать простые наблюдения…
Дуглас Хаббард

Литература

Нассим Талеб Одураченные случайностью. Скрытая роль шанса в бизнесе и обществе. – М.: Манн, Иванов и Фербер, 2011. – 320 с. Конспект: https://baguzin.ru/wp/?p=876

Дуглас Хаббард. Как измерить всё, что угодно. Оценка стоимости нематериального в бизнесе. – М.: Олимп-Бизнес, 2009. – 320 с. Конспект: https://baguzin.ru/wp/?p=2511

Использование метода Монте-Карло для расчета риска: https://baguzin.ru/wp/?p=3467

Моделирование методом Монте-Карло в Crystal Ball для Excel: https://baguzin.ru/wp/?p=3485

Анализ чувствительности в Excel: https://baguzin.ru/wp/?p=276