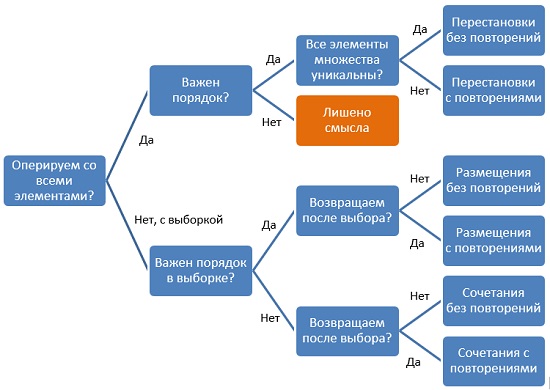
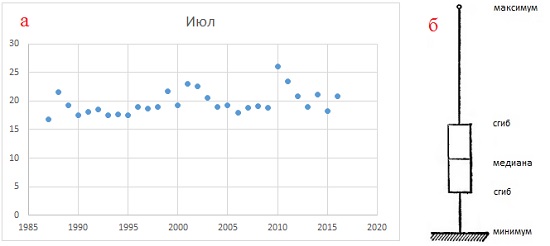
Центральная предельная теорема
Я часто сталкиваюсь с ситуацией, когда интересные научные концепции не используются на практике из-за сложности их представления. Одним из таких понятий является Центральная предельная теорема. Вот, что сказано в Википедии:
Центральные предельные теоремы – класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.
Звучит абстрактно… по крайней мере для меня. Переформулирую:
Центральная предельная теорема: независимо от формы распределения случайной величины средние выборок достаточного размера распределены нормально.
Если и эта формулировка мало что вам прояснила, не отчаивайтесь, изучите два примера.
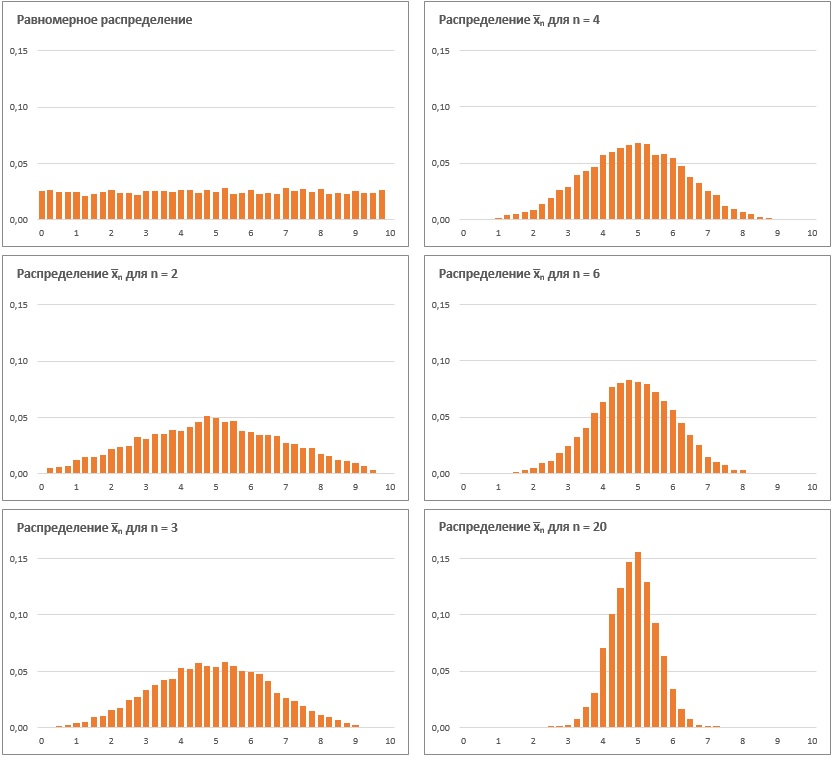
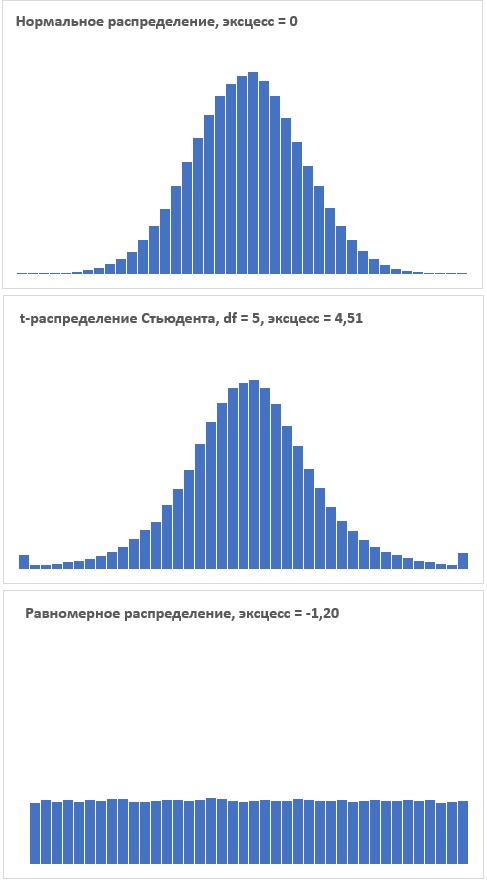
Рис. 1. Равномерное распределение случайной величины и распределение средних значений выборок разного размера